-
서론
최소 신장 트리(이하 MST)를 구하는 프림 알고리즘을 알아보자. 최소 신장 트리에대한 설명이 필요하다면 아래 글을 참고하도록 한다.
2024.08.13 - [알고리즘] - 최소 신장 트리
최소 신장 트리
신장 트리 (Spanning Tree)신장 트리는 다음과 같은 특징을 가진다.그래프의 모든 정점을 포함한다최소한의 간선의 개수를 가진다 ( 즉, 정점의 개수 - 1 개의 간선을 가진다)트리이기에 사이클을 가
devchive.tistory.com
프림 알고리즘
프림 알고리즘은 다음과 같은 순서를 가진다.
- 임의의 정점을 선택해 MST에 추가한다
- MST에 포함된 정점과 포함되지 않은 정점을 연결하는 간선 중 가장 비용이 적은 간선을 선택해 MST에 추가한다
- 최소 신장 트리에 V - 1개의 간선이 추가될 때 까지 2번 과정을 반복한다.
그림을보며 이해해 보자.

위와 같은 그래프에서 MST를 찾아보자. 임의의 정점인 1을 먼저 선택해 보겠다.
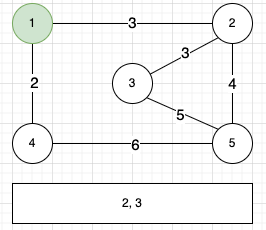
정점 1을 선택하고 연결된 간선들을 우선순위 큐에 넣어주었다. 이 우선순위 큐는 간선의 가중치를 기반으로 정렬된다.
연결된 간선중 가장 비용이 적은 4번 정점과 이어주는 간선을 선택한다.

4번 정점은 기존 MST에 속한 정점이 아니었으니 MST에 추가해주고 연결된 간선을 우선순위 큐에 넣어주었다. 다음으로는 2번 정점과 연결하는 비용 3 간선을 선택한다.
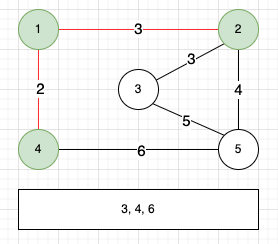
2번 정점 역시 기존 MST에 속하지 않았으니 MST에 추가하고 연결된 간선을 우선수위 큐에 넣어준다. 다음은 3번 정점과 연결하는 비용 3의 간선을 선택한다.
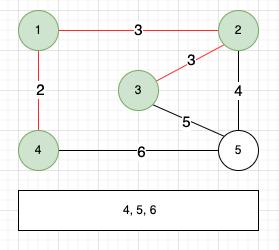
3번 정점도 기존 MST에 포함된 정점이 아니었으니 MST에 추가하고 연결된 간선을 우선순위 큐에 넣어준다. 다음으로는 5번 정점과 연결하는 비용 4의 간선을 선택한다.

5번 정점도 기존 MST에 속한 정점이 아니었으니 선택해준다. 이로써 V - 1 개의 간선을 선택하였고 모든 정점을 방문했다.
결과로 가중치의 총 합이 12인 MST가 나오게됐다.
문제풀이
백준 1197 문제를 프림 알고리즘을 이용해 풀어보자
https://www.acmicpc.net/problem/1197
public static List<ArrayList<Node>> adj = new ArrayList<>(); ... 중략 ... public static class Node implements Comparable<Node> { private int from, to, value; public Node(int from, int to, int value) { this.from = from; this.to = to; this.value = value; } @Override public int compareTo(Node o) { return value - o.value; } public int getTo() { return to; } public int getValue() { return value; } }인접 리스트로 그래프를 정의해주었다. 후에 가중치를 기반으로 우선순위 큐에 넣을 수 있도록 Node 클래스를 정의해주었다.
PriorityQueue<Node> pq = new PriorityQueue<>(); pq.add(new Node(0,1,0)); while(!pq.isEmpty()) { Node node = pq.poll(); int now = node.getTo(); if(visited[now]) continue; visited[now] = true; RESULT += node.getValue(); VISITED_COUNT++; if (VISITED_COUNT == N) break; ArrayList<Node> neighbours = adj.get(now); for(Node neighbour : neighbours) { if(visited[neighbour.getTo()]) continue; pq.add(neighbour); } }우선순위 큐를 사용해서 탐색한다. 초기에 1번 노드부터 시작하기 위해 가중치가 0인 Node 를 넣었다. 실질적으로 Node 의 from은 사용되지 않고있는데, 이런 문제처럼 총 가중치의 합만 구하는 문제의 경우 to, value 두가지만 가지도고 풀이가 가능하다.
전체 코드는 아래와 같다.
import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.util.ArrayList; import java.util.List; import java.util.PriorityQueue; import java.util.StringTokenizer; public class P1197 { public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); public static int N,M,VISITED_COUNT = 0, RESULT = 0; public static List<ArrayList<Node>> adj = new ArrayList<>(); public static boolean[] visited; public static void main(String[] args) throws IOException { StringTokenizer st = new StringTokenizer(br.readLine()); N = Integer.parseInt(st.nextToken()); M = Integer.parseInt(st.nextToken()); visited = new boolean[N+1]; for(int i = 0; i <= N; i++) { adj.add(new ArrayList<>()); } for(int i = 0; i < M; i++) { st = new StringTokenizer(br.readLine()); int from = Integer.parseInt(st.nextToken()); int to = Integer.parseInt(st.nextToken()); int value = Integer.parseInt(st.nextToken()); adj.get(from).add(new Node(from, to, value)); adj.get(to).add(new Node(to,from, value)); } PriorityQueue<Node> pq = new PriorityQueue<>(); pq.add(new Node(0,1,0)); while(!pq.isEmpty()) { Node node = pq.poll(); int now = node.getTo(); if(visited[now]) continue; visited[now] = true; RESULT += node.getValue(); VISITED_COUNT++; if (VISITED_COUNT == N) break; ArrayList<Node> neighbours = adj.get(now); for(Node neighbour : neighbours) { if(visited[neighbour.getTo()]) continue; pq.add(neighbour); } } System.out.println(RESULT); } public static class Node implements Comparable<Node> { private int from, to, value; public Node(int from, int to, int value) { this.from = from; this.to = to; this.value = value; } @Override public int compareTo(Node o) { return value - o.value; } public int getTo() { return to; } public int getValue() { return value; } } }'알고리즘' 카테고리의 다른 글
크루스칼 알고리즘 (0) 2024.08.13 최소 신장 트리 (0) 2024.08.13 위상 정렬 알고리즘 (0) 2023.08.02